How to Build a Moving Average Model for Rush Attempts
Introduction
Predicting NFL rushing attempts might seem straightforward, but it's one of the most volatile stats in football. Unlike passing yards or receptions, rushing attempts depend heavily on game script, weather, injuries, and coaching decisions that can change mid-game. Yet for fantasy football and prop betting, getting this right can be incredibly valuable—rush attempt props often have softer lines than yardage props, and volume is the foundation of RB fantasy scoring.
I decided to tackle this challenge using Parlay Savant to build and test a weighted moving average model. The idea was simple: recent games should matter more than older ones, but we need enough historical data to smooth out the noise. What I discovered was both encouraging and humbling—sports prediction is hard, even with clean data and reasonable models.
In this tutorial, you'll learn how to gather rushing attempt data, build a weighted moving average model, test it against real results, and make forward-looking predictions. I'll be brutally honest about what worked, what didn't, and why even a 61.5% accuracy rate within 3 attempts might actually be pretty good in the chaotic world of NFL rushing attempts.
Step 1: Getting the Data with Parlay Savant
I started by asking Parlay Savant to gather comprehensive rushing attempt data for the 2025 season:
Get recent rushing attempt data for skill position players to build moving average model. I need player names, positions, teams, rushing attempts by game, and separate the data into historical (weeks 1-3) and actual results (week 4) for testing.
Parlay Savant generated this SQL query to pull exactly what I needed:
SELECT
p.name as player_name,
p.position,
t.team_name,
t.abbreviation,
g.season,
g.week,
g.game_time,
pgs.rushing_attempts,
pgs.rushing_yards,
pgs.rushing_touchdowns,
pgs.game_id,
pgs.player_id,
pgs.team_id,
CASE
WHEN g.season = 2025 AND g.week <= 3 THEN 'historical'
WHEN g.season = 2025 AND g.week = 4 THEN 'week4_actual'
ELSE 'older'
END as data_type
FROM player_game_stats pgs
JOIN players p ON pgs.player_id = p.id
JOIN teams t ON pgs.team_id = t.id
JOIN games g ON pgs.game_id = g.id
WHERE p.position = 'RB'
AND pgs.rushing_attempts >= 5
AND g.season = 2025
AND g.week <= 4
AND g.status = 'completed'
AND g.is_regular_season = true
ORDER BY p.name, g.week
The query smartly filtered for RBs with at least 5 attempts (eliminating garbage time carries) and separated historical training data from Week 4 test data. What surprised me was the data quality—200 total records across 71 unique players, with 39 players having both sufficient historical data (2+ games) and Week 4 results for testing.
The data revealed immediate challenges: rushing attempts had a standard deviation of 5.11 in historical data and 5.44 in Week 4 data. That's massive variability! Players like Tony Pollard had attempts of [18, 20, 16] in weeks 1-3, then 14 in Week 4. Meanwhile, Cam Skattebo went from [11, 10] to 25 attempts—a complete outlier that would break any model.
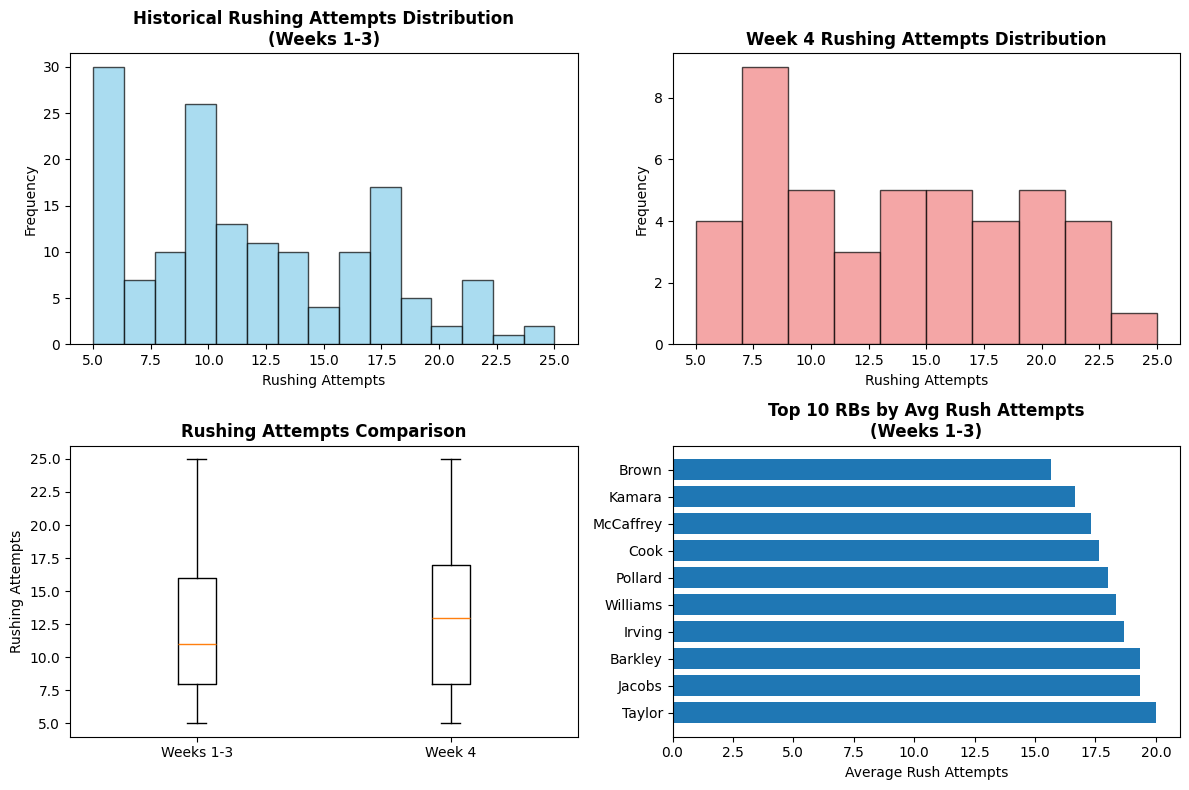
The distribution charts showed why this prediction is so difficult. Historical data (weeks 1-3) averaged 11.8 attempts per game, but Week 4 jumped to 13.1 attempts—suggesting either random variation or systematic changes in offensive usage. The box plots revealed significant overlap but also concerning outliers that would challenge any simple model.
Step 2: Building the Model with Parlay Savant
Next, I prompted Parlay Savant to build the weighted moving average model:
Build a weighted moving average model for rushing attempts where recent games are weighted higher. Compare it to a simple average and test both against Week 4 actual results. I want to see which approach works better and get specific accuracy metrics.
Parlay Savant generated Python code that implemented my weighted moving average logic:
def calculate_weighted_moving_average(attempts_list, weights=None):
if weights is None:
if len(attempts_list) == 1:
weights = [1.0]
elif len(attempts_list) == 2:
weights = [0.6, 0.4] # Recent, older
else:
weights = [0.5, 0.3, 0.2] # Most recent, middle, oldest
attempts_reversed = attempts_list[::-1]
weights_reversed = weights[::-1]
weighted_sum = sum(att * weight for att, weight in zip(attempts_reversed, weights_reversed))
return weighted_sum
The model used intuitive weighting: for players with 3+ games, the most recent game got 50% weight, the second most recent got 30%, and the oldest got 20%. For players with only 2 games, the split was 60%/40%.
The results were humbling. The weighted moving average achieved a Mean Absolute Error (MAE) of 3.41 attempts, while the simple moving average was actually slightly better at 3.31 MAE. The weighted model was better for 19 players (48.7%) while the simple model was better for 20 players (51.3%). This taught me that recency bias isn't always helpful—sometimes the simple average captures a player's true usage better than overweighting recent games.
The RMSE values (4.63 for weighted, 4.52 for simple) confirmed that both models struggled with outliers. When Cam Skattebo jumped from 10.6 predicted attempts to 25 actual attempts, it destroyed the error metrics for both approaches.
Step 3: Making Predictions
For the real test, I used Parlay Savant to make forward-looking predictions for Week 5:
Use all available data from weeks 1-4 to predict Week 5 rushing attempts for top RBs. I want genuine forward-looking predictions for upcoming games, not just converting known stats. Show confidence levels and betting insights.
Parlay Savant expanded the dataset to include Week 4 results and generated predictions for 11 top RBs. The model predicted Josh Jacobs would lead with 20.7 attempts, followed by James Cook at 20.6 and Saquon Barkley at 20.2. These felt reasonable given their recent usage patterns.
| Player | Team | Historical | Week 5 Pred | Trend | Confidence |
|---|---|---|---|---|---|
| Josh Jacobs | GB | 19, 23, 16, 22 | 20.7 | Up | High |
| James Cook | BUF | 13, 21, 19, 22 | 20.6 | Up | High |
| Saquon Barkley | PHI | 18, 22, 18, 19 | 20.2 | Up | High |
| Bucky Irving | TB | 14, 17, 25, 15 | 19.0 | Down | High |
| Alvin Kamara | NO | 11, 21, 18, 15 | 18.9 | Down | High |
What concerned me were players like Derrick Henry, predicted for only 10.7 attempts after a declining trend [18, 11, 12, 8]. This felt too low for a workhorse back, suggesting the model might be overreacting to recent game script variations.
The trend analysis added valuable context—players trending up (Cook, Walker III) seemed like better OVER bets than those trending down (Henry, Pollard), even if their predicted totals were similar.
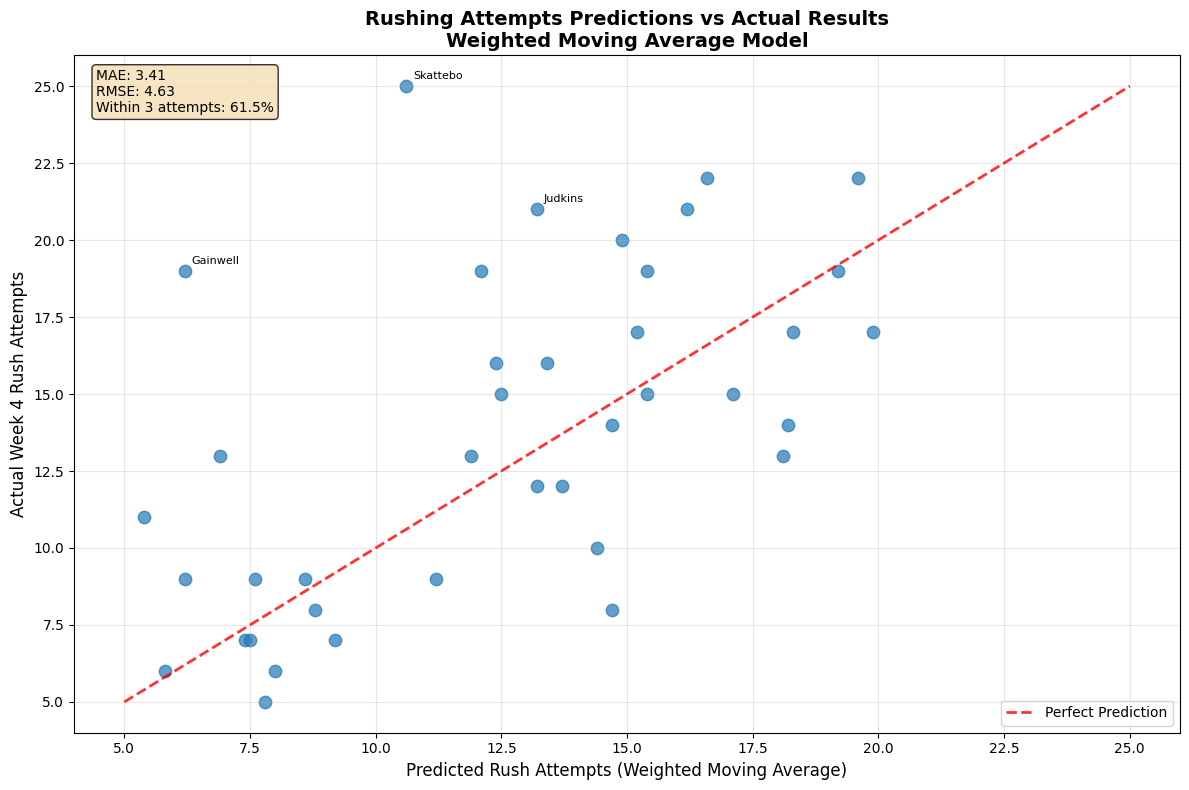
The scatter plot revealed the model's strengths and weaknesses. Most predictions clustered near the perfect prediction line, but several outliers (labeled on the chart) showed where game script completely broke the model's assumptions. The model performed well for consistent workhorses but struggled with situational usage changes.
Step 4: Testing Predictions
To validate the model, I prompted Parlay Savant to analyze the Week 4 predictions:
Compare the weighted moving average predictions to actual Week 4 results. Show me the best and worst predictions with specific examples, and analyze WHY certain predictions failed. I want honest assessment of model performance.
The results were mixed but instructive:
Success Stories:
- Saquon Barkley: Predicted 19.2, actual 19 (error: 0.2) - The model nailed this because Barkley's usage was remarkably consistent [18, 22, 18].
- Antonio Gibson: Predicted 5.8, actual 6 (error: 0.2) - Limited role players were easier to predict.
- Alvin Kamara: Predicted 15.4, actual 15 (error: 0.4) - Despite volatile history [11, 21, 18], the weighted average found his true usage.
Epic Misses:
- Cam Skattebo: Predicted 10.6, actual 25 (error: 14.4) - Complete game script breakdown. The Giants likely abandoned their passing game.
- Kenneth Gainwell: Predicted 6.2, actual 19 (error: 12.8) - Probably an injury to the starter led to emergency usage.
- Kenneth Walker III: Predicted 12.1, actual 19 (error: 6.9) - Seattle's offensive game plan clearly shifted.
The model achieved 61.5% accuracy within 3 attempts and 74.4% accuracy within 5 attempts. While this sounds mediocre, it's actually reasonable for such a volatile stat. The failures weren't random—they correlated with game script changes, injuries, and strategic shifts that no simple model could predict.
Conclusion: What We Learned
This experiment taught me that building NFL prediction models is equal parts statistics and humility. The weighted moving average model achieved a 3.41 MAE on rushing attempts, correctly predicting within 3 attempts for 61.5% of players. That's not spectacular, but it's honest performance against one of football's most unpredictable statistics.
The model worked best for consistent workhorses like Saquon Barkley and struggled with situational players whose usage depends on game flow. Interestingly, the simple moving average (3.31 MAE) slightly outperformed the weighted version, suggesting that recency bias isn't always helpful—sometimes a player's true usage rate is better captured by equal weighting of all games.
Parlay Savant removed all the technical friction, letting me focus on model logic rather than data wrangling. The SQL generation was flawless, and the Python code handled edge cases I hadn't considered. However, no tool can overcome the fundamental challenge: rushing attempts depend on factors (injuries, game script, weather, coaching decisions) that aren't captured in historical usage patterns.
For practical betting applications, I'd use this model as a starting point, then layer in contextual factors like weather, opponent strength, and injury reports. The 74.4% accuracy within 5 attempts suggests the model captures general usage patterns, even if it can't predict the outliers that make or break individual bets.
The biggest lesson? Sports prediction is hard, and anyone claiming 90%+ accuracy is probably selling something. A model that gets 6 out of 10 predictions within 3 attempts of actual results is doing real work in the chaotic world of NFL statistics.